First successful demonstration of quantum error correction of qudits for quantum computers

In the world of quantum computing, the Hilbert space dimension—the measure of the number of quantum states that a quantum computer can access—is a prized possession. Having a larger Hilbert space allows for more complex quantum operations and plays a crucial role in enabling quantum error correction (QEC), essential for protecting quantum information from noise and errors.

A recent study by researchers from Yale University published in Nature created qudits—a quantum system that holds quantum information and can exist in more than two states. Using a qutrit (3-level quantum system) and a ququart (4-level quantum system), the researchers demonstrated the first-ever experimental quantum error correction for higher-dimensional quantum units using the Gottesman–Kitaev–Preskill (GKP) bosonic code.

Most quantum computers on the market usually process information using quantum states called qubits—fundamental units similar to a bit in a regular computer that can exist in two well-defined states, up (1) and down (0) and also both 0 and 1 at the same time, due to quantum superposition. The Hilbert space of a single qubit is a two-dimensional complex vector space.

Since bigger is better, in the case of Hilbert space, the use of qudits instead of qubits is gaining a lot of scientific interest.

Qudits could make demanding tasks such as building quantum gates, running algorithms, creating special “magic” states, and simulating complex quantum systems easier than ever. To harness these powers, researchers have spent years building qudit-based quantum computers with the help of photons, ultracold atoms and molecules and superconducting circuits.

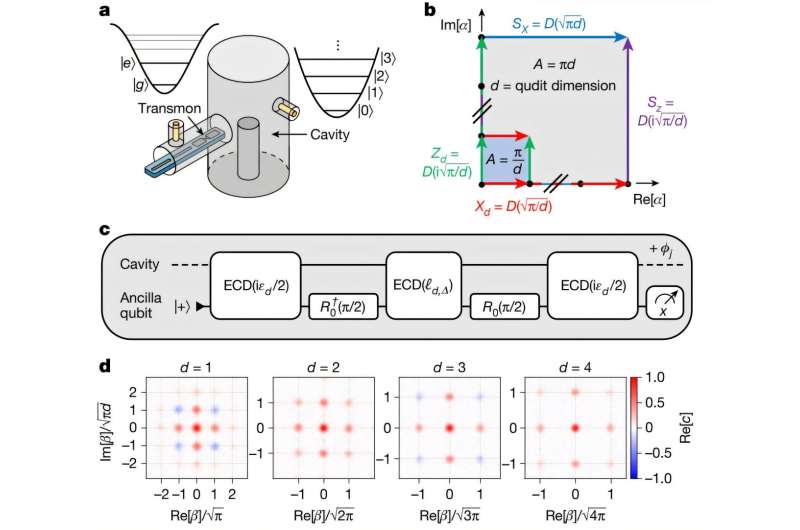
The reliability of quantum computing is heavily dependent on QEC, which safeguards fragile quantum information from noise and imperfections. Yet, most experimental efforts in QEC are focused exclusively on qubits, and so qudits took a backseat.

The researchers on this study presented the first ever experimental demonstration of error correction for a qutrit and a ququart, using the Gottesman–Kitaev–Preskill (GKP) bosonic code. To optimize the systems as ternary and quaternary quantum memories, the researchers opted for a reinforcement learning algorithm, a type of machine learning that utilizes a trial and error method to find the best way to correct errors or operate quantum gates.

The experiment pushed past the break-even point for error correction, showcasing a more practical and hardware-efficient method for QEC by harnessing the power of a larger Hilbert space.

The researchers note that the increased photon loss and dephasing rates of GKP qudit states can lead to a modest reduction in the lifetime of the quantum information encoded in logical qudits, but in return, it provides access to more logical quantum states in a single physical system.

The findings demonstrate the promise of realizing robust and scalable quantum computers and could lead to breakthroughs in cryptography, materials science, and drug discovery.

© 2025 Science X Network